LinkedList

Here is the linked list. It looks like this.

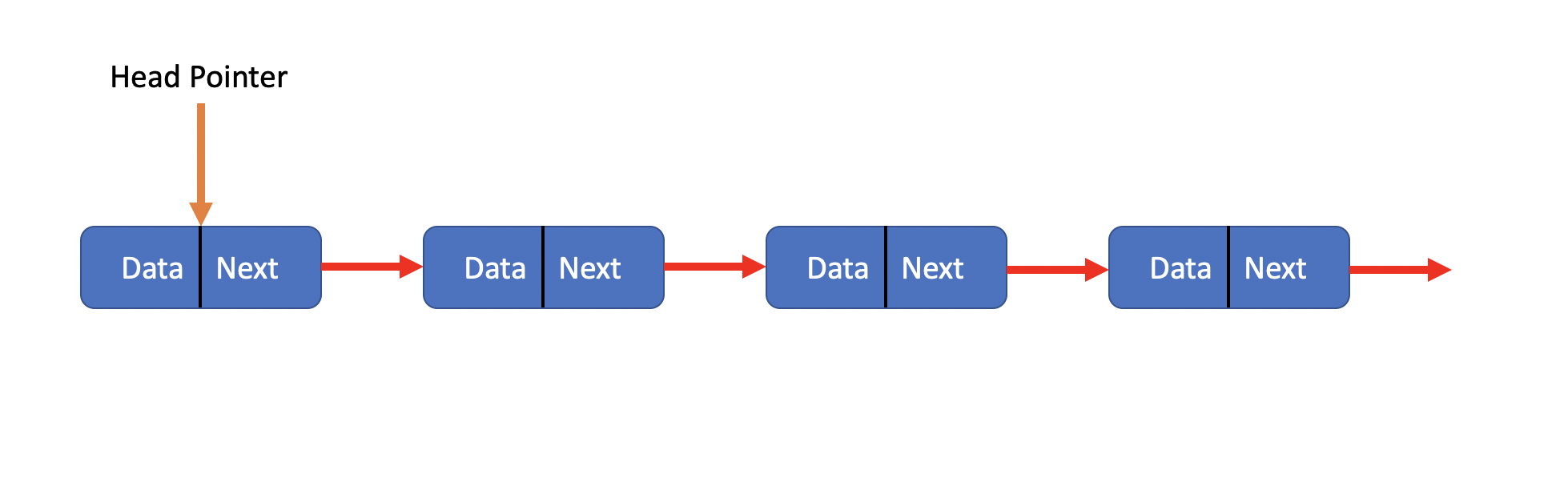
In order to avoid the linear cost of insertion and deletion, we need to ensure that the list is not stored contiguously. By using this kind of list, we can make the cost of insertion and deletion be O(1).
The linked list consists of a series of structures, which are not necessarily adjacent in memory.

Each node contains the element and a pointer points to the next node, we call it Next pointer, And the last node’s Next pointer points to NULL. And ANSI C specifies that NULL is zero.

In my version, I put a head node to save the length of the linked list.

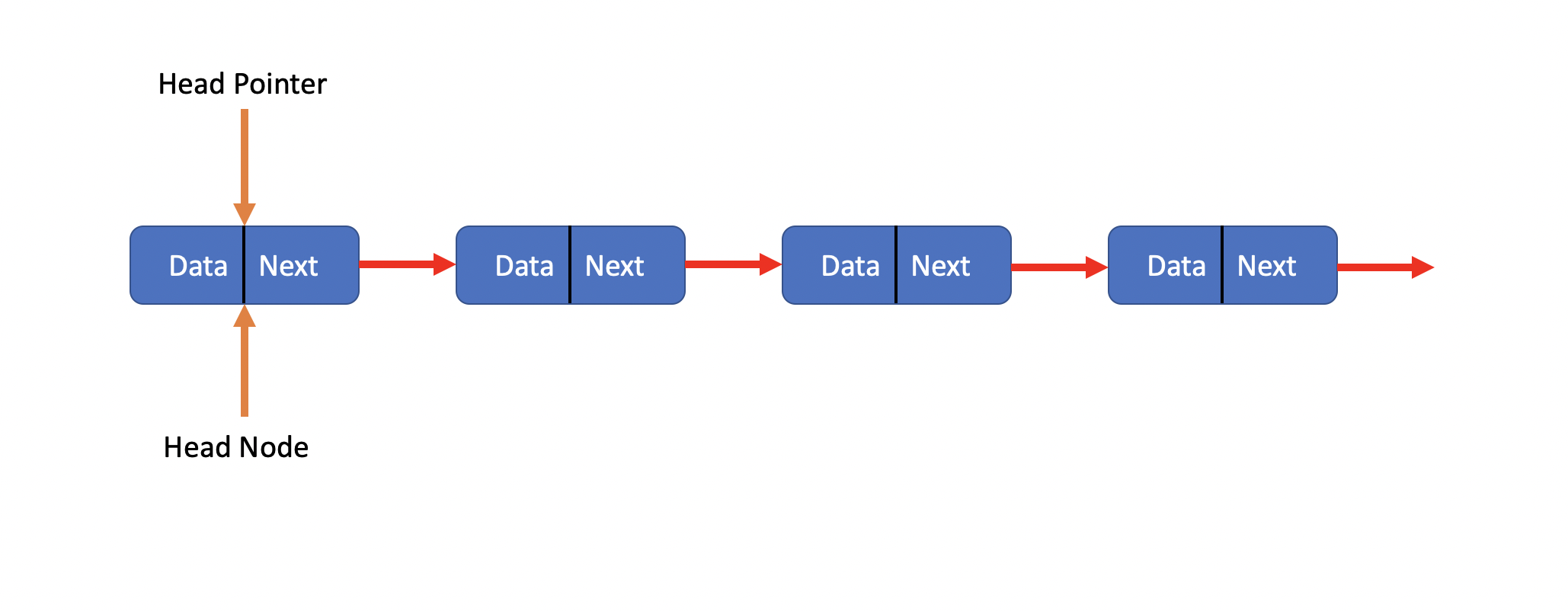
Now we can see the operations of LinkedList.

Operations

• Insert
• Delete

Insert

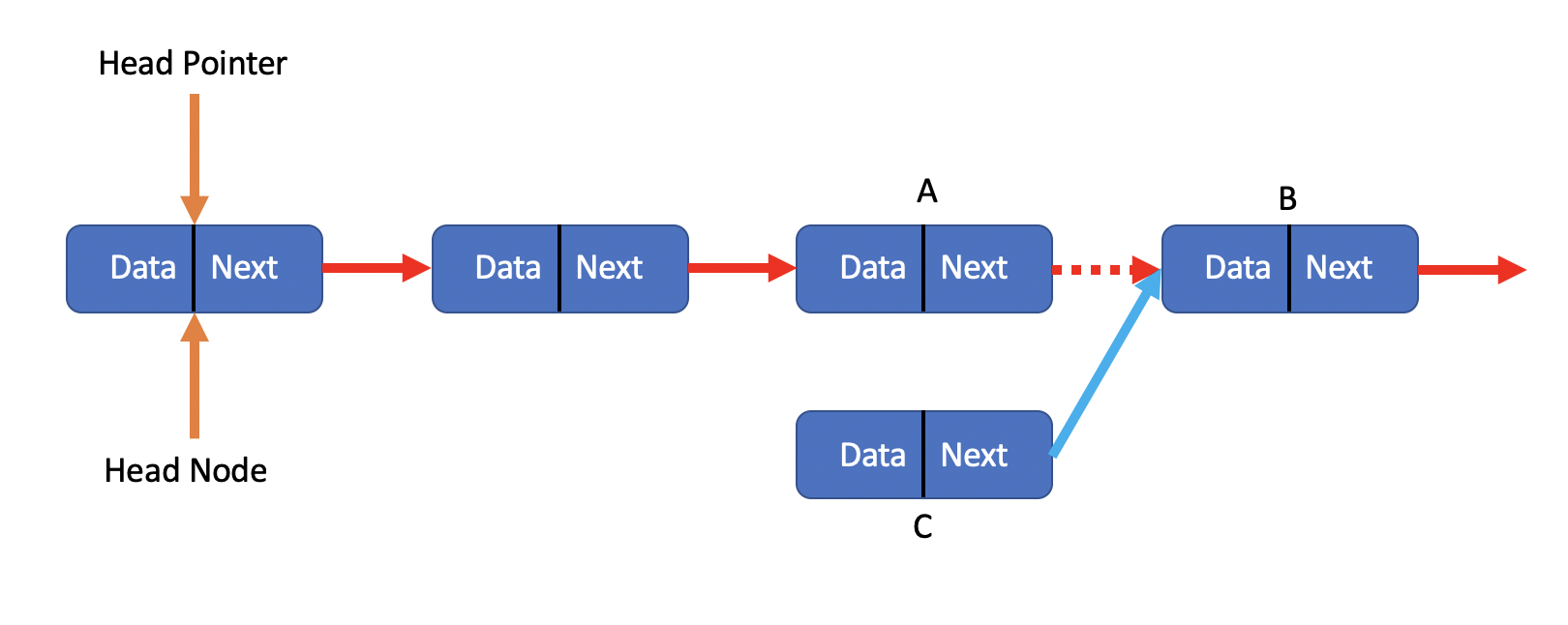
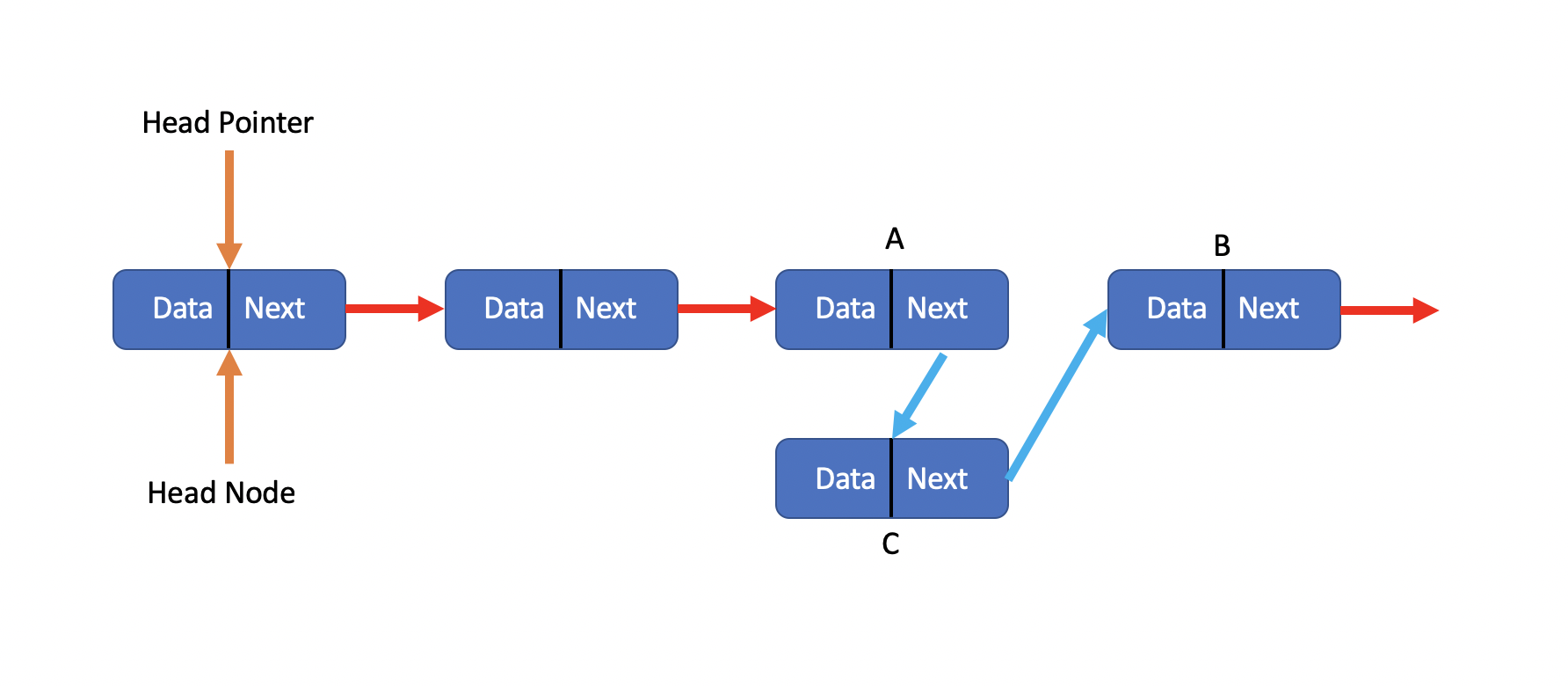
It’s the first step of the insert operation.

As we can see, we got Node A, B, C, and the C is the newest node we wanna insert into this list. First we make the Next pointer of C equals Next pointer of A, then the C node’s Next Pointer points to node B.

second step, we let the A’s Next pointer points to our new node C.

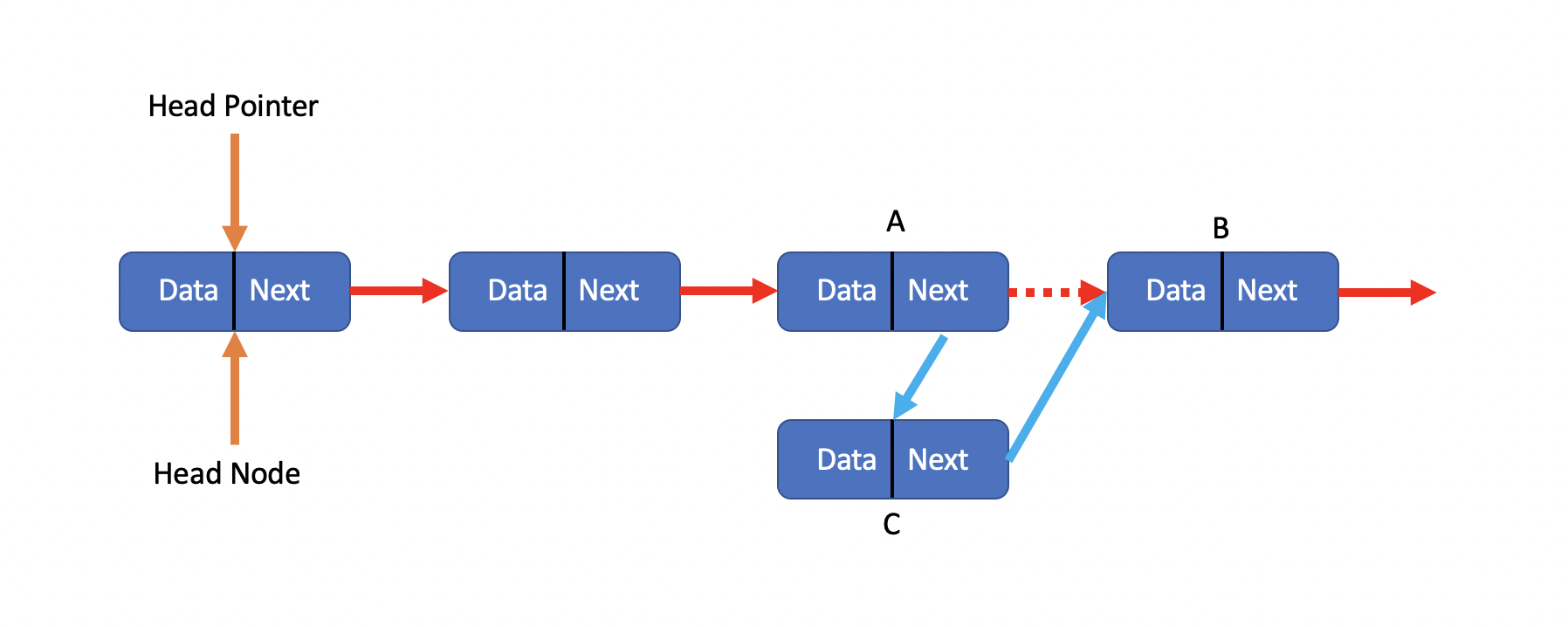
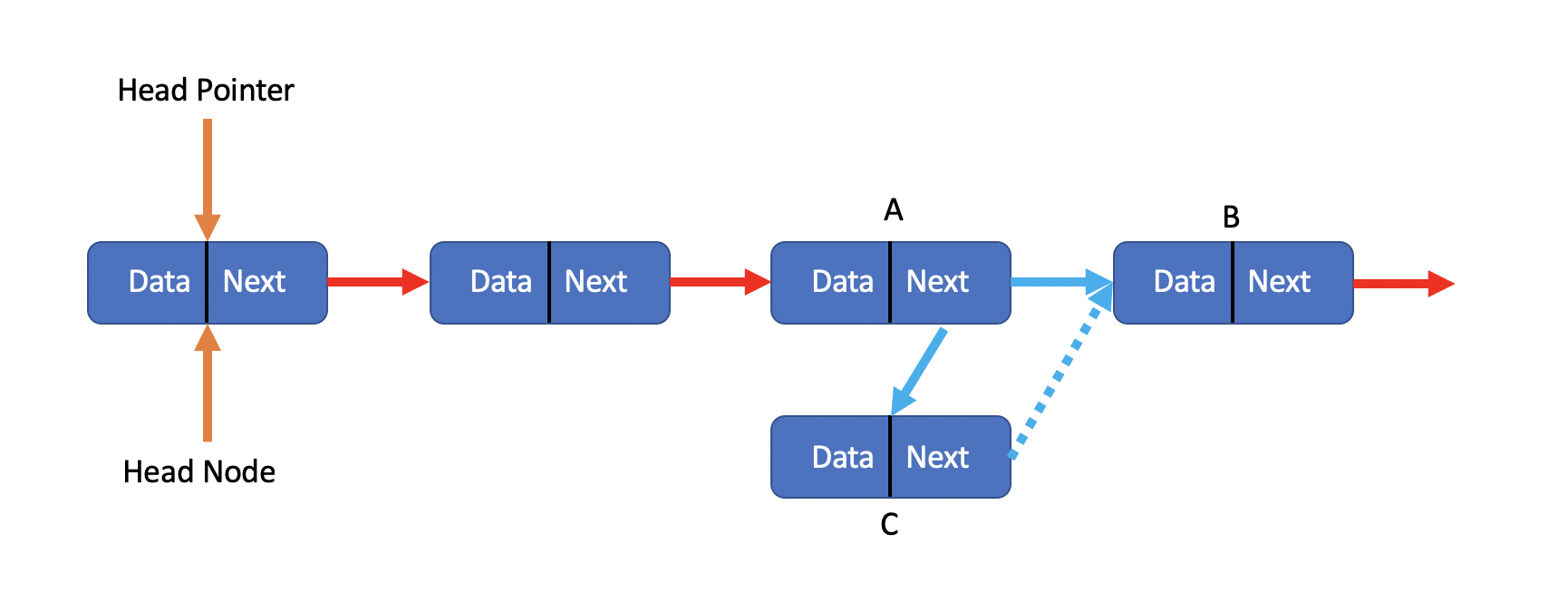
Finally, we finished it.

Insert Succeed!!

Let’s take a look at the code.

• Insert at the tail

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

// Insert a value after all elements
void
Insert(List L, ElementType value)
{
	Position NewNode, LastNode;
	NewNode = (struct Node *) malloc(sizeof (struct Node));
	if (NewNode == NULL)
		FatalError("Insert failed. No enough room!!");
	LastNode = L->Head;
	NewNode->Value = value;
	NewNode->Next = NULL;
	if (LastNode == NULL)
		L->Head = NewNode;
	else
	{
		while(LastNode->Next != NULL)
			LastNode = LastNode->Next;
		LastNode->Next = NewNode;
	}
	L->Size += 1;
}

• Insert at given index

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

// Insert a Value at the index you give
void
InsertAt(List L, int index, ElementType value)
{
	if (index > L->Size || index < 0)
		FatalError("Illegal index"); 
	if (index == L->Size)
		Insert(L, value);
	else {
		PtrToNode NewNode = (struct Node *)malloc(sizeof(struct Node));
		if (NewNode == NULL)
			FatalError("No Enough room!");
		NewNode->Value = value;
		Position TmpPointer;
		TmpPointer = L->Head;
		if (index == 0)
		{
			NewNode->Next = L->Head;
			L->Head = NewNode;
		}
		else
		{
			int i = 0;
			while (++i < index)
			{
				TmpPointer = TmpPointer->Next;
			}
			NewNode->Next = TmpPointer->Next;
			TmpPointer->Next = NewNode;
		}
		L->Size += 1;
	}
}

Delete

We’ll show two steps of delete operation.

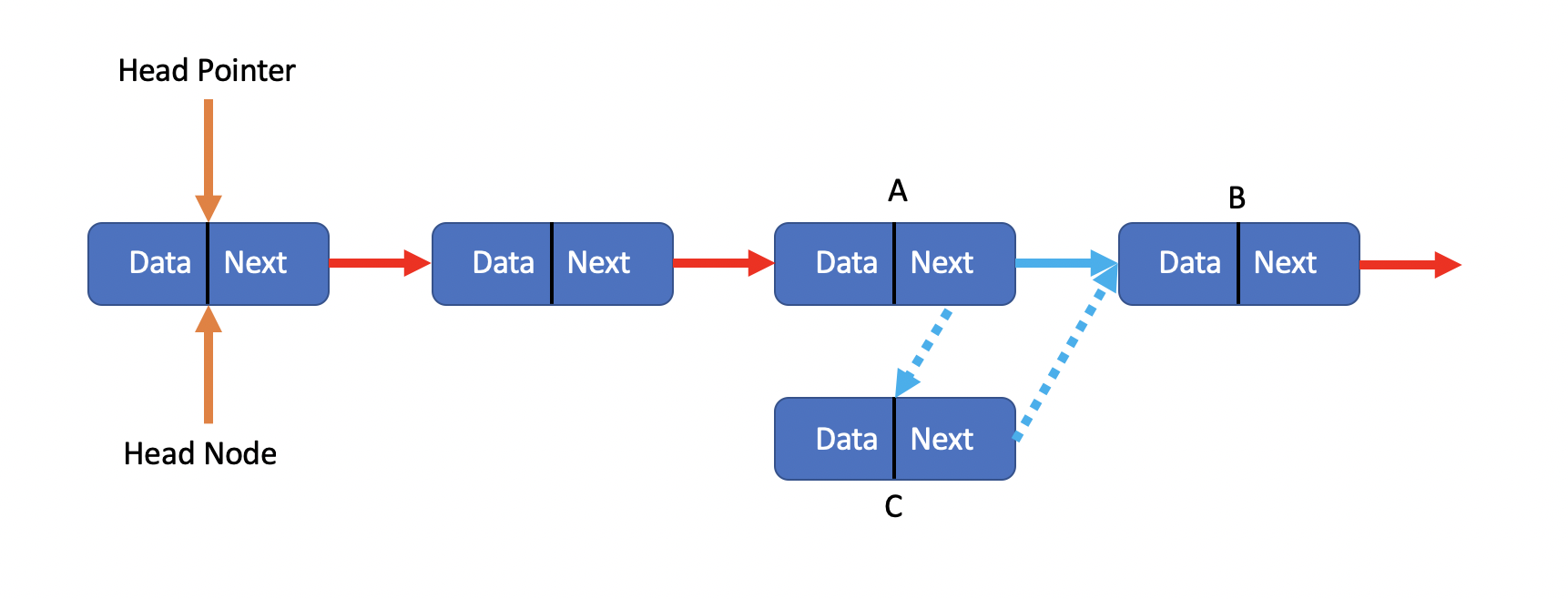
First step, we let the node A’s Next pointer equals the Next pointer of node C.

Because we just get one Next pointer for each node, so, it just make no pointer points to node C.

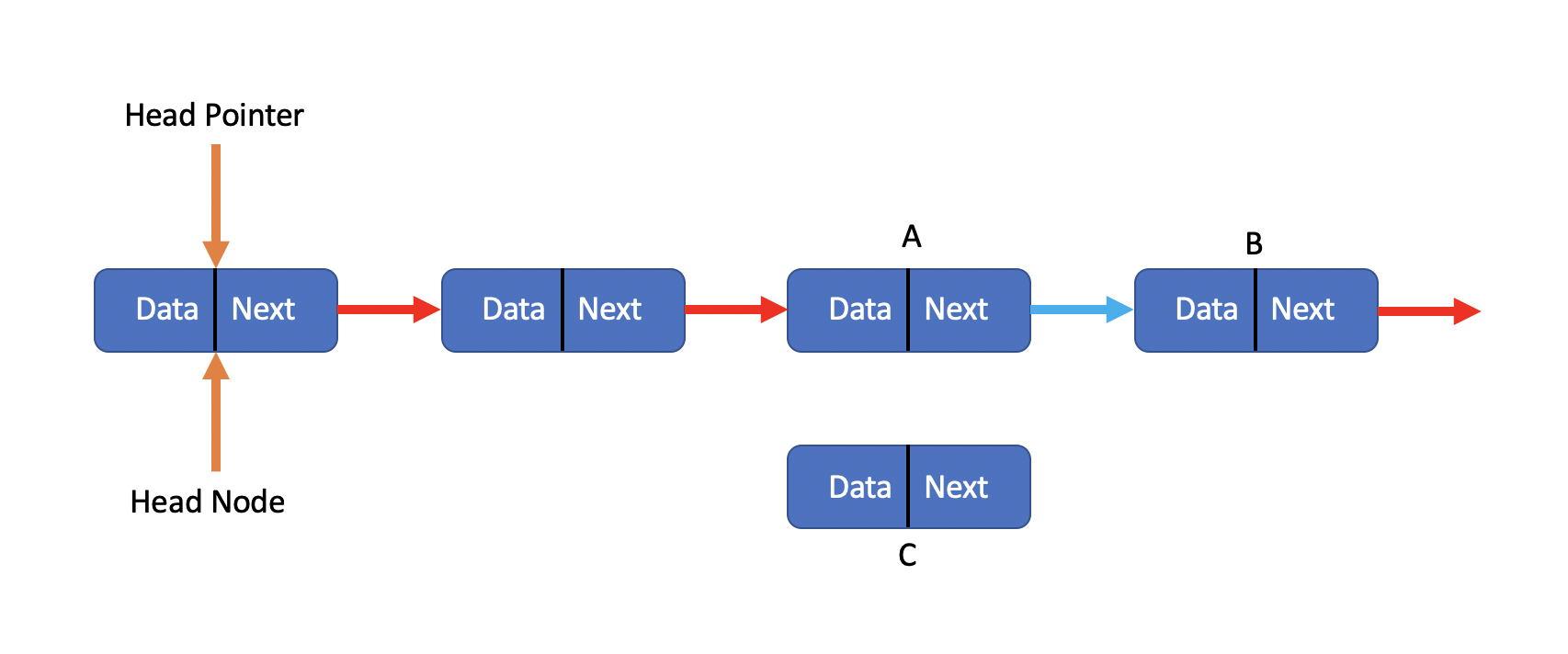
So delete Succeed!!

• Delete at the tail

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

// Delete the last node of list L
void
Delete(List L)
{
	if (L == NULL || L->Size == 0)
		FatalError("Delete failed. Please try to create a list and insert some nodes into it.");
	Position P, Previous;
	P = L->Head;
	if (L->Size == 1)
	{
		L->Head = NULL;
	}
	else
	{
		while (P->Next != NULL)
		{
			Previous = P;
			P = P->Next;
		}
		Previous->Next = NULL;
		L->Size -= 1;
	}
	free(P);
}

• Delete at the given index

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

// Delete the node at the index you give
void
DeleteAt(List L, int index)
{
	if (index > L->Size - 1)
		FatalError("Illegal index");
	Position P, NewNext;
	P = L->Head;
	if (index == 0)
	{
		NewNext = P->Next;
		L->Head = NewNext;
		free(P);
	}
	else
	{
		int i = 0;
		while (++i < index)
			P = P->Next;
		NewNext = P->Next->Next;
		free(P->Next);
		P->Next = NewNext;
	}
	L->Size -= 1;
}

Conclusion

We know that if you just calculate the cost of insertion or deletion, you’ll find T(n) = O(1).
But you know if we wanna insert or delete a value with specify index, it’ll cost O(n) in whole operation. But the cost of insertion or deletion still is O(1). Here, we just talk about the cost of insertion or deletion.

• ← Previous Post
• Next Post →